Synthesizer-Diplom (Synthesetechnik/en, Wavetables)
Digitale Synthesizer
3. Synthesetechniken
3.2 Hybridsysteme / Mischformen
3.2.1 Wavetable-Synthese (Wavescanning / Wavesequencing)
Die im „Wave“, dem „Microwave“ und dem „Microwave 2“ der Firma Waldorf verwendete Synthese soll hier nun näher -und stellvertretend für viele andere- exemplarisch beschrieben werden. Auch liegt es nahe, diese Geräte näher zu beleuchten, da es sich (neben Quasimidi) um eine der wenigen deutschen Synthesizer-Herstellerfirmen handelt. Dabei wird der volldigitale Microwave 2 den Hybridsystemen Wave und Microwave gegenübergestellt, die allesamt als Digitalsynthesizer in der Geschichte bereits länger verzeichnet sind: Anfangs noch von Wolfgang Palms Firma „PPG“ aus Deutschland entwickelt (Wavecomputer 360/340, Wave 2 – 2.3 & Waveterm; Erscheinungsjahre:1978, ´81-´84) und schließlich von Waldorf aufgegriffen und erweitert, gipfelt in dem zur Zeit aktuellen Microwave 2, der nach Veröffentlichung dieser Arbeit herauskommen wird (ca. März ´97).
„Hybrid“ ist eine Mischform aus Digital- und Analogtechnik: Die (zwei) Oszillatoren sowie die komplette Wavetablesynthese- Technik ist dabei schon digital ausgeführt, auch Hüllkurven und LFOs.. Das Signal gelangt über eine Mischeinheit in eine analoge Filtersektion, im Microwave ein 24 dB/Okt. LPF (Tiefpaßfilter), der durch Chips der Firma Curtis gebildet wird. Danach folgt die Vertärkersektion und die Panoramaeinheit (Stereobalance-Modul = Panning), in welcher die gewünschte Stereoposition nach dynamischer Lautstärkebearbeitung eingestellt/moduliert wird.
Die Filtereinheit ist beim Wave um einen resonanzlosen „12dB Hochpaß“ erweitert worden, sowie um einige digitale und analoge Zusätze bereichert (zusätzliche Hüllkurve, Analogeingänge, etc…).
Der Microwave 2 ist hingegen „ganz und gar“ digital und besitzt zwei digitale Multimodefilter: Mit 24dB/Okt. als HPF/LPF oder 12dB/Okt. Flankensteilheit auch als BPF verwendbar. „Filter 2“ hat lediglich 6dB/Okt., aber auch die Wahlmöglichkeit zwischen HPF und LPF und „festere Verdrahtung“ (weniger Modulation!), im Gegensatz zu Filter 1. Wichtig zu wissen ist: Die digitalen Filter klingen natürlich nicht identisch mit den analogen Curtisfiltern im „alten“ Microwave, da, wie schon erwähnt, Verzerrungen „chaotisch“ und anders „mathematisiert“ werden müssen (was in Analogtechnik unnötig ist, sondern einfach schon „da“ ist)! Es gibt aber heutzutage keine Argumentationsmöglichkeit mehr, daß „digital“ auch „schlechter“ sein muß, es wird nur schlicht etwas „anders“ klingen (aufgrund der völlig anderen Konstruktion)!
Die Oszillatoren können, wie in subtraktiven Synthesizern, auch moduliert und in ihrer Tönhöhe justiert werden. Die entscheidende Andersartigkeit gegenüber subtraktiven Geräten ist das „Wavescanning“ oder auch „Wavetable“ (Wellensatztabelle) genannte Verfahren: Ein Wavetable ist eine Sammlung von 64 Wellenformen („Waves“), welche wiederum aus 128 wählbaren Wellenformdatenschritten, hier „Samples“ genannt, bestehen. Die einzelnen Waves sind tatsächlich jeweils ein „Durchlaufzyklus“ (Periode) einer vollständigen Welle, welche in einem Computer verändert (editiert) werden können. Die drei Wellenformen Triangle (Dreieck), Square (Rechteck) und Saw (Sägezahn) sind in manchen Geräten in dieser Reihenfolge als Wellen 61 – 63 generell immer anwählbar, wobei die gewählte Wavetable die restlichen Waves liefert (beim Wave sind diese Waves 61-63 frei definierbar). Dies ist lediglich eine Festlegung des Herstellers und könnte softwaremäßig auch im Microwave geändert werden.
Die wirkliche Synthese ist nun dergestalt, daß ein achtstufiger Hüllkurvengenerator („Wave-Envelope“, welche 8 Zeiten und 8 Pegel hat, die nacheinander angefahren werden) diese Wellentabelle „durchfährt“. Sie schaltet also bei entsprechendem aktuellem Steuerwert der Hüllkurve die dazugehörige Wave proportional zum Steuerwert um und erzeugt den nichtstatischen Klang. Da auch längere Hüllkurven-Zeiten möglich sind, kann so auch ein längerer Verlauf mit unterschiedlichen Wellenformen durchfahren werden. Da ein einfaches Umschalten äußerst „ruckelig“ klingen würde, treten hier die „Samples“, die den Waves „untergeordnet“ sind, ein, denn sie bilden eine echtzeitberechnete, interpolierte „Brücke“ zwischen den einzelnen Waves und sorgen somit für ein weiches Überblenden. Ein Parameter „Wave Mode“ kann von stepped („stufig“) auf smooth („weich“) geschaltet werden. Dies sorgt dafür, die „Samples“ (Wellenperiodendaten einer Wave) zwischen den Waves über den „Computerzwischenspeicher“ möglichst gleichformig (entsprechend der o.a. Einstellung) „überlaufen“ zu lassen. Werden weniger Waves in ein Wavetable gesetzt (per Computer editierbar) können hier, durch mehr Platz für die Zwischenstufen, weichere Übergänge erzeugt werden, denn die fehlenden Waves werden durch Interpolation (ohne Speicherverlust) errechnet und „virtuell“ an den freien Platz gesetzt.
Die Hüllkurve besitzt durch ihre Achtstufigkeit eine große Bandbreite der Variation einer „Wellenfahrt“ und die Möglichkeit, eine Schleife (Loop) zwischen zwei beliebige Stufen zu setzen. Die Modulation aller Zeiten gemeinsam und zusätzlich aller Pegel gemeinsam ist ebenfalls möglich. Ein noch größeres Potential ergibt sich durch die Tatsache, daß alle Parameter der Waldorf – Geräte mindestens ein- bis zweimal beliebig moduliert werden können, so auch die Wavetablefahrt!! Der zweite Oszillator muß sich zwar derselben Wavetable bedienen, kann jedoch frei darin „herumfahren“ und andersartig moduliert werden.
Ein zweiter Aspekt ist die freie Wahl des „Startsample“, also der Phasenlage der Wellenperiode. Wenn diese auf „free“ steht, wird eine zufällige Phasenlage gewählt.
Mindestens 32 Wavetables gibt es. Dazu sind einige benutzerdefinierbar (z.B.: 12 Stück im Microwave).
Die Auflösung der Wavetable-Technik ist 8 Bit, also 256 mögliche Schritte, auf der Auslenkungs-/(y-)Achse. Um andere Töne zu erreichen, wird die Ausleserate verändert und interpoliert (Werte weggelassen bei niedrigen, hinzugefügt bei hohen Tönen!). Diese ist von ca.160kHz auf ca.44kHz geändert worden, denn das 8fache Oversampling wurde hier verwendet (eine Technik im Zusammenhang mit Wandlern zur „Verbesserung“ – Hier muß ich auf die Fachliteratur verweisen).
Dies ist auch beim Sampling der Grund, warum Töne, die im Original auf „A“ liegen, eine Oktave tiefer schon „verfremdet“ wiedergegeben werden, da die Ausleserate dabei reduziert ist, für darüberliegende Oktaven aber zu viele Werte fehlen, um der höheren Ausleserate genügend Werte zu „liefern“. Die Waldorfgeräte haben den sogenannten „Micky-Maus-Effekt“ nicht (im Gegensatz zu Samplern), da hier genügend Werte errechnet (interpoliert) werden, die Samplern nicht zur Verfügung stehen und sogar die „Interpolationsqualität“ eingestellt werden kann. Oft wird auch die Auslesegeschwindigkeit in Samplern nicht geändert (nur Interpolation).
Doch zurück zum System: Da beim Microwave 2 nicht nur eine gespiegelte Halbwelle benutzt wird (64 Bytes), sondern eine ganze (128 Bytes), ein Relikt aus einer Zeit, in der Speicher noch sehr teuer waren, gibt es eine Verbesserung für viele Sounds (z.B. Pulsbreitenmodulation!). Hieraus ist auch die „Sample“ Länge von 128 zu erklären.
Ein weiteres klangerweiterndes Mittel kann die Mischstufe sein. Diese hat eine 3 Bit Auflösung; also kann von 0 bis 7 geregelt werden. Auch ein Noisesignal (Rauschgenerator) läßt sich hier zuregeln (ebenfalls von 0-7). Dies alles ist beim Microwave 2 höher aufgelöst (128 Stufen) und erlaubt bessere Ein- und Ausblendung der drei Klangquellen. Die Besonderheit der Mischeinheit ist nicht nur die Modulierbarkeit, sondern daß sich ab der Summe der beiden Oszillatorenlautstärken von „8“ eine Verzerrung einsetzen läßt (Beim Microwave 2 ist dieser Wert entsprechend höher).
Dies alles wird mit einem Motorola 8 Mhz – 68000 Prozessor erzeugt, der etwa die Leistung eines Atari ST hat -der Microwave 2 wird mit einem 68331 und einem DSP 56303 bestückt und läuft mit 21 Mhz, was erheblich schneller ist, und zudem dieses Prozessorderivat auch Wandler enthält (kosten- / platzsparend).
Auch die zwei LFOs und die zwei Hüllkurven, sowie die achtstufige Wave-Envelope wird durch den Prozessor generiert. Der LFO 1 hat noch eine „Minihüllkurve“, die es ermöglicht, diesen ein- („Attack“) und auszublenden („Decay“) und vorher noch zu verzögern („Delay“). Die Symmetrie ist einstellbar. Dies ist das Verhältnis von „Wellenberg“ („positiver“ Teil) zu „Wellental“ („negativer“ Teil) in einer Periode. Die Humanizefunktion bringt einen von 0-7 einstellbaren Zufälligkeitseinfluß auf die LFO-Geschwindigkeit mit ein, welche ebenfalls regelbar ist und im typischen LFO – Bereich „bis ca. 25Hz“ liegt. Diese ist im Microwave 2 auf 100Hz angehoben worden, womit interessante Amplituden-, Filter-, sowie Wavemodulationen möglich sind, die FM-ähnlich klingen können! Die LFOs, haben fünf Wellenformen: Zufall, Dreieck, Sinus, Rechteck und Sample & Hold („S/H“). Diese (S/H-) Funktion nimmt einen Zufallswert an und hält diesen, bis der „LFO – Geschwindigkeitszeitraum“ abgelaufen ist, während die Einstellung „Zufall“ (random) ständige Änderungen produziert. Die LFOs lassen sich miteinander synchronisieren (Gleichlauf), womit rhythmisch abhängige Modulationen möglich sind. Auch gibt es eine Phasenverschiebung gegeneinander, die in Grad eingestellt wird. Der LFO1 kann zusätzlich in seiner Geschwindigkeit und Intensität auch moduliert werden.
Die restlichen Hüllkurven sind in „ADSR“-Bauweise aufgebaut (siehe „3.1.1 Baugruppen“); die Filterhüllkurve hat noch einen Delayparameter vorgeschaltet, der den Pegel auf Null hält, bis die Attackzeit beginnt („DADSR“). Alle Hüllkurvenparameter sind modulierbar, was extrem flexibel ist und mit sehr wenigen anderen Geräten überhaupt machbar ist! Der Wave und Microwave 2 haben eine zusätzliche erweiterte Hüllkurve, dafür keine Minihüllkurve in LFO1 und kleine Abweichungen bezüglich der Modulation des Delayparameters. Es gibt, wie im Wave auch im Microwave 2, sogenannte Modifier, die verschiedene Bearbeitungen der Modulationssignale zulassen (mathematisch / logische Operationen, Verzögerungsgeneratoren, u.a..) und eine Minihüllkurve ebenfalls simulieren lassen, kurz: vergleichbaren und verbesserten Ersatz bieten. Die Modulationen werden im Microwave 2 über eine (auf 16 Verbindungen) begrenzte Modulationsmatrix bedient, die das Konzept des „allesmodulierenden Monsters“ zugunsten der Rechenzeit verringert (es zählt die „Updatezeit“, in der alle Werte neu berechnet sind – diese ist zwingend höher für die Geschwindigkeiten der LFOs etc..). Die Oszillatoren können dafür im Microwave 2 synchronisiert werden (Obertonveränderung)!! Außerdem gibt es Ringmodulation, -diese erlaubt metallische Klänge, wie oben beschrieben.
Die Oszillatoren-, Wavetable-, Verstärker-, Panorama- und Filterparameter etc… sind allesamt modulierbare Ziele, oft sogar mehrfach. Einige haben „Seitensteuereingänge“ („Sidechains“ / „Ctrl. Input“), die die Modulationsquelle durch eine weitere Modulationsquelle steuern können. Z.B. LFO1 wird durch das Modulationsrad in seiner Intensität gesteuert, dieser LFO1 moduliert die Resonanz des Filters. Das Ergebnis ist eine Steuerung der LFO-Modulationsintensität auf den Resonanzparameter durch das Modulationsrad.
Als (Modulations-)Quellen stehen (u.a.) zur Verfügung: LFOs, Hüllkurven, MIDI-Controller, die Hüllkurve von LFO1, Keytrack, Anschlagdynamik… Außerdem gibt es zusätzlich oft benutzte, festverdrahtete Modulationsverbindungen, wie Filter-Cutoff (Filtereckfrequenz)-Steuerung durch Filterhüllkurve. Die Oszillatoren können nicht als Modulationsquelle zur Verfügung gestellt werden. Dies ist auch nicht üblich, außer in FM- oder AM-Geräten, die aber wiederum keine Wavetablesynthese anbieten. Durch die schnellen Microwave 2 – LFOs und die Ringmodulation / Sync(hronisation) wird aber soetwas trotzdem möglich!
Es gibt noch einige Funktionen für das spezielle Stimmen und Skalieren, sogar ein Programm zur Reinstimmung der Oszillatoren ist im Microwave zu finden: sobald ein Akkord gespielt wird, werden sie auf die „Reinstimmung“ dieses Akkordes korrigiert, dies wird „Hermode-Tuning“ (hmt) genannt und kann in „Keys 3/95“ gehört / nachgelesen werden. Die restlichen Funktionen werden nicht näher beschrieben… sie dienen weiterer Organisation und subtilerer oder speziellerer Klangformung und sind unterschiedlich in den Geräten realisiert. Auch die „SysEx-Steuerung“ (= spezielle Befehle über die MIDI Schnittstelle zur kompletten Echtzeitsteuerung eines ganz speziellen Gerätes eines Herstellers) oder die Editierzwischenspeicher (mehrere!) sind keine Normausstattung, dienen aber ebenfalls der schnellen Rahmensprengung dieser Arbeit).
Ein letzter, aber sehr kreativer Punkt ist die Computereditierbarkeit der Waves und Wavetables. Es gibt ein additives Verfahren und die sogenannten UPAWs (User Programmable Algorithmic Wavetable = Benutzerprogrammierbare algorithmische Wellentabelle). Im additiven Modus kann eine Wellenform durch Veränderung der ersten 64 harmonischen Teiltöne eingestellt werden (die x-ten ganzzahligen Vielfachen des Grundtons im harmonischen Spektrum). Die resultierende Wave wird dargestellt und kann in einem Wavetable verwendet werden. Der Clou hierbei ist die Dynamisierung der (nun nicht mehr festen) Einzelspektren, die ja beliebig kombiniert werden können.
Die UPAWs benutzen verschiedene Syntheseformen wie FM Sy nt he s e, W av es ha pi ng (e tc. ..) u m W av etables zu errechnen, dabei gibt man zuvor die zugehörigen Parameter an und läßt so einen Wellensatz durch den Computer „offline“ (nicht in Echtzeit) ausrechnen. Eine Mischung mit „normalen“ Waves ist allerdings nicht möglich. Der Waldorf Wave kann zudem ein Sample in den Speicher holen und es in ein Wavetable umrechnen lassen, dabei wird das Sample in soviel gleiche Teile aufgeteilt, wie es Waves in einem Wavetable gibt, und für diese „Gesamtteilzeit“ wird ein additives Spektrum errechnet (mit der „Fourieranalyse“) und eine Wavetable gebildet.
Der analysierte Zeitraum ist:
Samplelänge dividiert durch Anzahl der Waves in einem Wavetable.
Wenn das fertige Ergebnis nun durchfahren wird, hat man ein
 „ungefähres“ Abbild des analysierten Samples. Diese und andere Offlinealgorithmen können benutzt werden, manche im Wave sogar direkt nach Knopfdruck abhörbereit! Der Wave arbeitet mit einem Multiprozessorsystem (MC68000) und hohen Taktfrequenzen. Beim Computer und Microwave (2) – Verbund ist die Übertragung und Verarbeitung noch „dazwischen“ und „bremst“ etwas.
„ungefähres“ Abbild des analysierten Samples. Diese und andere Offlinealgorithmen können benutzt werden, manche im Wave sogar direkt nach Knopfdruck abhörbereit! Der Wave arbeitet mit einem Multiprozessorsystem (MC68000) und hohen Taktfrequenzen. Beim Computer und Microwave (2) – Verbund ist die Übertragung und Verarbeitung noch „dazwischen“ und „bremst“ etwas.
Soviel zu den wichtigsten Waldorfer Techniken. Das Wavesequencing der Korg Wavestation funktioniert nach einem ähnlichen System, allerdings mit Samples: Diese werden „anstatt“ der Wellentabellen durch die Hüllkurve angewählt und bei Wechsel zu einem anderen Sample (durch einen anderen Modulationssteuerwert) in das dazugehörige, nächste Sample überblendet, hier wirklich überblendet und nicht „gemorpht“. Man hat hier auch eine Liste der Einzelsamples zu erstellen, was dem Waldorf – System prinzipiell nahe ist.
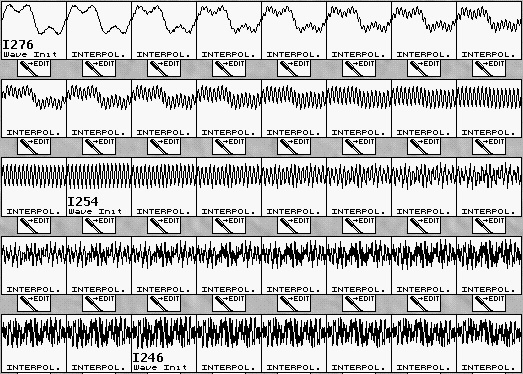
Hier ein Beispielausschnitt eines solchen Wavetable-Wellenverlaufes. Die mit Nummern bezeichneten „Waves“ sind am Computer konstruiert, alle anderen sind interpolierte „Waves“:
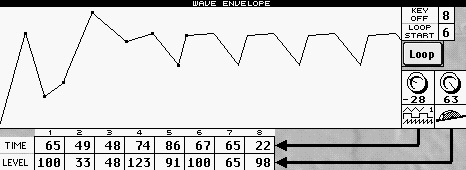
Links: Eine „geloopte “ Wave-Envelope (Hüllkurve) zwischen dem sechsten und achten Segment. Jeder Punkt markiert ein Segment (siehe Wertetabelle darunter). Ohne Loop würde der Verlauf nach dem achten Segment beendet.
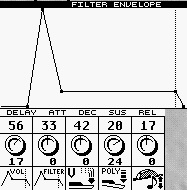
Rechts: Filterhüllkurve mit Modulationsquellen (Piktogramme).
nachtrag: dies ist der Microwave 2 bzw. Microwave XT (zum zeitpunkt des schreibens der diplomarbeit gab es den XT noch nicht!!)
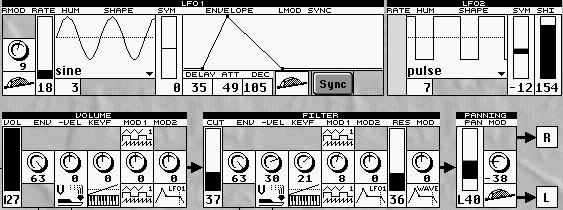 Die Oszillator-,Wave-, Misch- und LFO-Sektion des Microwave mit allen Modulationquellen.
Die Oszillator-,Wave-, Misch- und LFO-Sektion des Microwave mit allen Modulationquellen.
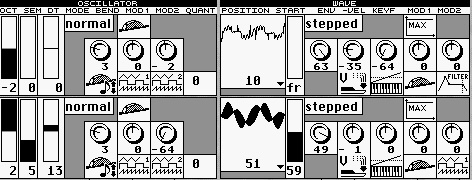
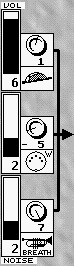
Mischer: Osc.Osc.2 Noise: rechts.
Die beiden LFO´s des WALDORF Microwave v.l.n.r.: LFO1,Minihüllkurve und LFO2
von l. nach r. : Lautstärke, Filter und Panorama – Einstellungen
ZURÜCK ZUM HAUPTMENÜ.. weiter..
©96/97 mic.irmer (www.moogulator.com) – kopieren (auch Auszugsweise) ohne Genehmigung nicht gestattet.



